2023년 3월 모의고사 수학 선택과목 미적분(23번~30번) 손글씨 해설, 등급컷, 오답률을 정리하였습니다. 수학 공통문항(1번~22번), 확률과 통계, 기하에 대한 손글씨 해설은 아래 글을 참고해 주세요. 글의 순서는 다음과 같습니다.
2023년 고3 3월 모의고사 수학(미적분) 등급컷 및 오답률
2023년 고3 3월 모의고사 미적분 손글씨 해설
2022년 고3 모의고사 미적분 손글씨 해설
2023년 고3 3월 모의고사 수학(미적분) 등급컷 및 오답률
2023년 고3 3월 모의고사 미적분 등급컷과 오답률(1위~15위)입니다. ebs에 공개된 내용을 정리하였으며, 오답률은 조사하는 기관에 따라 다소 차이가 있을 수 있습니다. 2023년 3월 모의고사 전 과목 문제와 해설, 등급컷을 아래 글에서 확인하실 수 있습니다.
| 등급 | 원점수 | 표준 점수 |
백분위 | 오답률(EBS)(문항번호/오답률) | ||||||
| 미적분 | 순위 | 번호/오답률 | 순위 | 번호/오답률 | ||||||
| 1 | 77 | 138 | 96 | 1 | 22번/96.6% | 9 | 14번/58.4% | |||
| 2 | 66 | 128 | 89 | 2 | 30번/93% | 10 | 27번/58% | |||
| 3 | 55 | 118 | 77 | 3 | 20번/88.9% | 11 | 13번/55.1% | |||
| 4 | 38 | 103 | 60 | 4 | 21번/84% | 12 | 12번/54.3% | |||
| 5 | 23 | 89 | 46 | 5 | 29번/75.6% | 13 | 18번/52.2% | |||
| 6 | 15 | 82 | 24 | 6 | 28번/72.3% | 14 | 11번/49.8% | |||
| 7 | 12 | 79 | 14 | 7 | 19번/62.6% | 15 | 17번/45.8% | |||
| 8 | 7 | 75 | 4 | 8 | 15번/59.5% | |||||
2023년 고3 3월 모의고사 미적분 손글씨 해설
3월 미적분 시험은 범위가 작아 수능 시험의 형태와는 조금 차이가 있습니다. 그러나 해당 범위에서 학습해야 할 문제들로 잘 구성되어 있습니다.
2023년 고3 3월 모의고사 미적분 26번: 극한의 성질에 관련된 문제입니다. lim를 분배법칙처럼 적용하려면 반드시 수렴한다는 조건이 있어야 합니다. 아래 문제에서 주어진 형태의 꼴을 만들고 lim를 나눌 때 반드시 수렴하는지 확인하는 습관이 필요합니다.

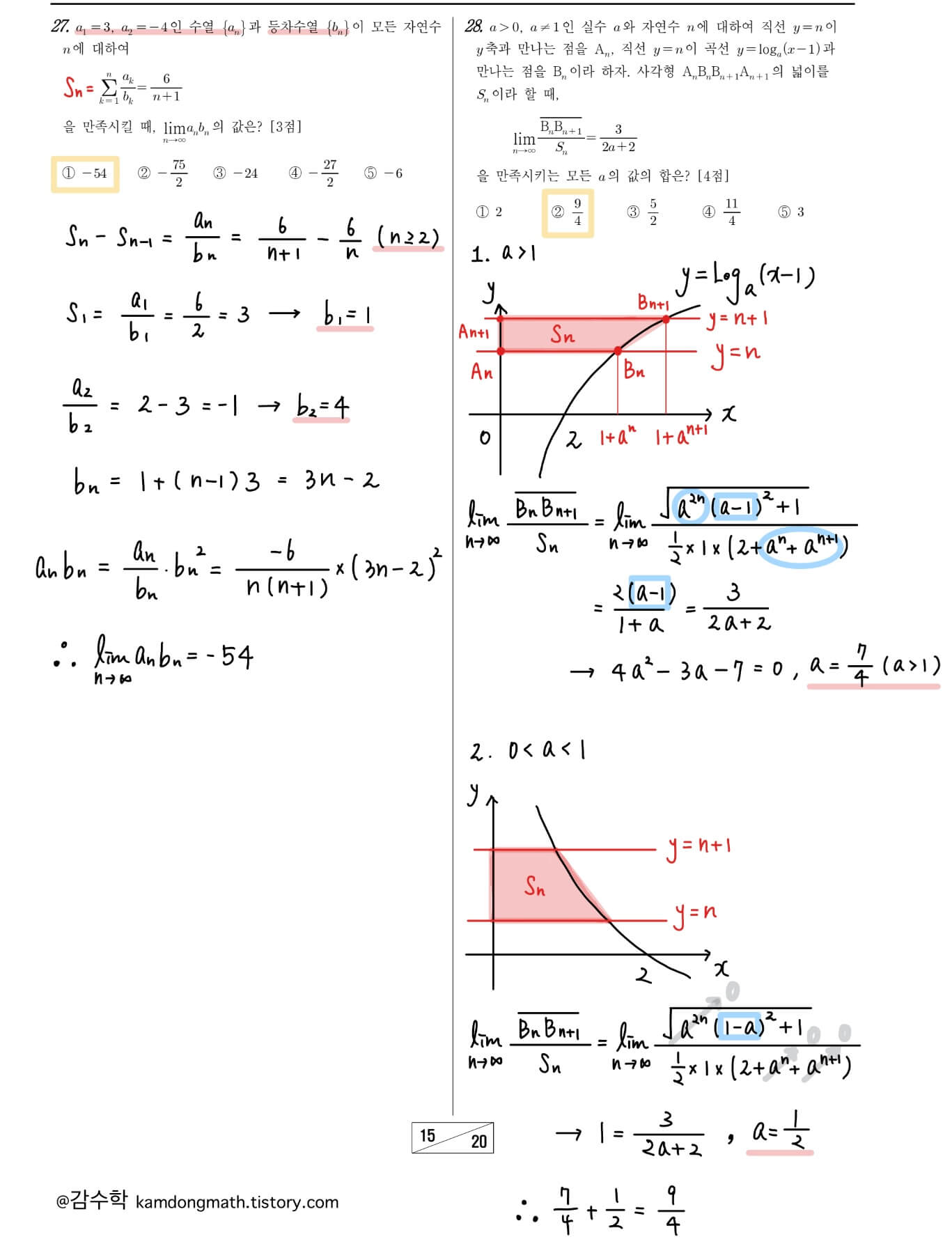
2023년 고3 3월 모의고사 미적분 27번: 등차수열의 합 문제입니다. 수열의 합 Sn에서 일반항 an을 구하는 식은 n이 2 이상인 경우에만 만족하며, a1=S1을 이용하여 구해야 합니다. 실수하지 않도록 주의해야 할 부분입니다.
2023년 고3 3월 모의고사 미적분 28번: a의 범위에 따라 그래프가 달라지므로 나눠서 생각해야 합니다. 또한 범위에 따라 극한값의 꼴이 다르므로 구하는 과정도 차이가 있습니다. 극한값을 구하는 과정에서 가장 우선 생각해야 할 부분은 꼴(무한대/무한대, 0/0, 무한대-무한대 등등)입니다.
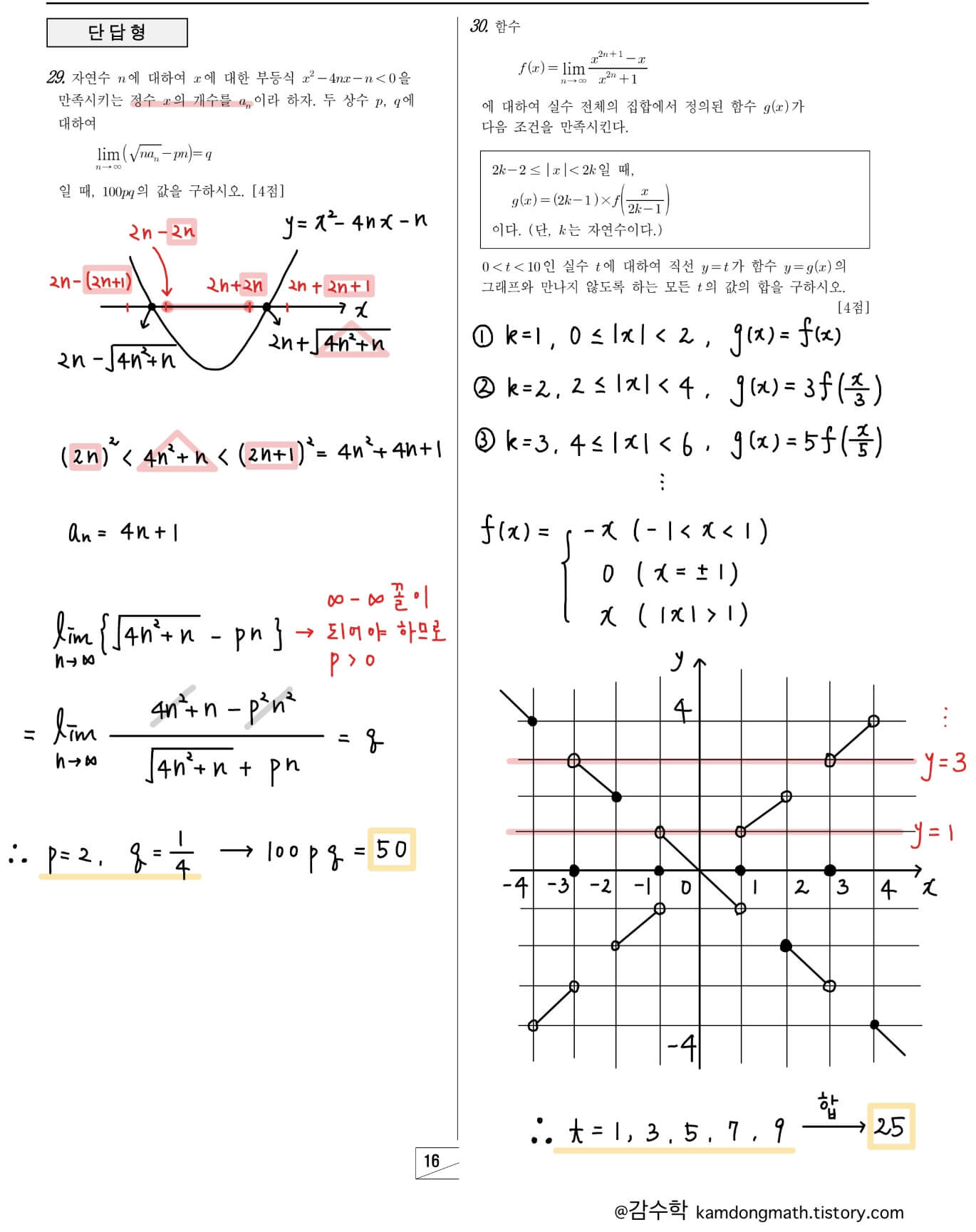
2023년 고3 3월 모의고사 미적분 29번: 무한대-무한대 꼴의 극한문제입니다. 극한값을 구하기 전 an을 구해야 합니다. 제곱수를 이용하여 an을 구할 수 있으며, 극한값에서 p값을 구하는 과정의 정확한 이해(무한대-무한대 꼴이 극한값이 존재하기 위한 조건)가 필요합니다.
2023년 고3 3월 모의고사 미적분 30번: 오답률 2위(93%) 수열의 극한으로 정의된 함수 문제입니다. 범위 때문에 수능 30번과는 문항의 유형과 난도가 차이가 있지만 수열의 극한으로 정의된 함수를 공부하기에 좋은 문제입니다. 조건에 맞는 그래프를 그리고, 최종적으로 t가 홀수 일 때, 조건을 만족함을 추론할 수 있어야 합니다.
2022년 고3 모의고사 미적분 손글씨 해설
2022년에 시행된 고3 모의고사와 수능 미적분 문제에 대해서 손글씨풀이, 등급컷, 오답률이 정리되어 있습니다.




댓글