2022년 7월 30일에 시행된 2023학년도 사관학교 1차 시험 수학 선택과목 미적분(23번~30번) 손글씨 해설입니다. 공통문제(1번~22번), 선택과목 확률과 통계, 기하 문제의 해설은 아래 링크를 활용해주세요.
사관학교 기출문제 및 수학 해설
사관학교 국어, 수학, 영어 기출문제 파일과 수학 손글씨 해설입니다. 필요에 따라 활용해주세요.
2023학년도(2022년) 사관학교 수학 미적분 해설
총 8문항(23번~30번) 중 27번부터 30번까지 문제의 풀이를 첨부하였습니다. 학습에 참고해주시고 풀이에 오류나 궁금한 부분이 있으시면 댓글을 달아주세요.
2023학년도(2022년) 사관학교 미적분 27번
수능 및 모의고사에서 매번 출제되고 있는 도형의 무한 등비급수 문제입니다. 공비를 구하는 것은 어렵지 않고 첫 번째 항을 구하는 것이 조금 까다롭게 느껴질 수도 있습니다. 도형문제를 해결할 때는 닮음, 합동을 잘 관찰하여 해결하는 것이 중요합니다. 같은 유형의 문제를 충분히 연습할 수 있도록 파일을 만들었으니 아래 글을 참고해주세요.

2023학년도(2022년) 사관학교 미적분 28번
28번 문제는 많이 출제된 내용입니다. 이때, y=atanx와 y=sinx의 교점이 상수 아닌 a에 의해 결정되는 함수 k(a)로 생각할 수 있어야 합니다. 풀이에서는 양변을 미분하여 해결하였으나 적분을 하여 f(a)를 구한 다음에 다시 미분을 하여 해결할 수도 있습니다.

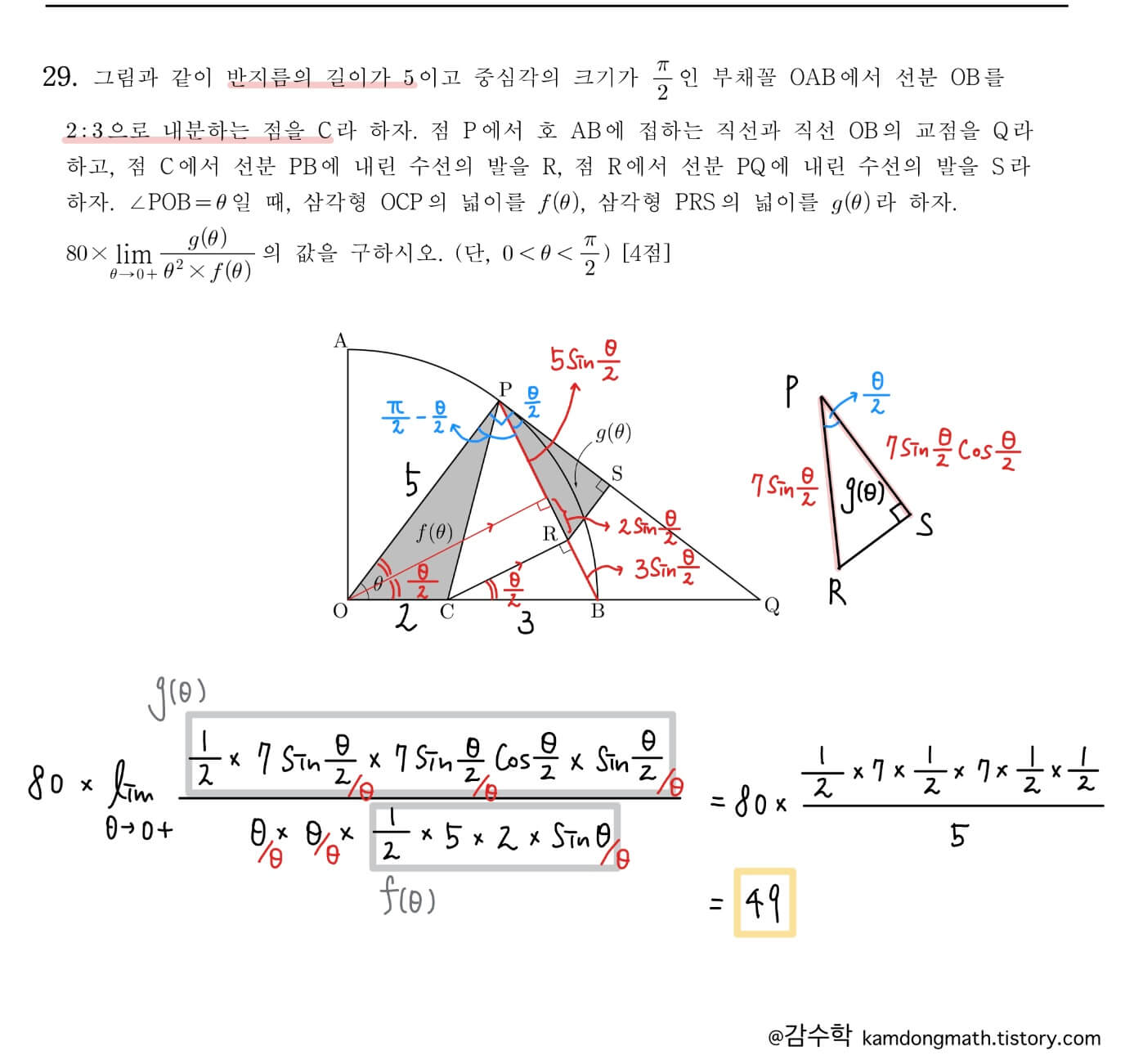
2023학년도(2022년) 사관학교 미적분 29번
항상 출제되고 있는 도형과 함수의 극한 문제입니다. 비교적 쉽게 출제되었으며 닮음을 이등변 삼각형과 삼각형의 닮음을 이용한다면 두 도형의 넓이를 어렵지 않게 구할 수 있습니다. 연습이 더욱 필요하신 분은 아래 글을 활용해주세요.
2023학년도(2022년) 사관학교 미적분 30번
(가) 조건을 이용해 f(x)를 구할 수 있으며 (나) 조건에서 그래프 사이의 관계를 찾아낼 수 있어야 합니다. 최종적으로 접하는 순간이 b가 최대가 되는 순간이 됩니다. 추가적으로 이차함수와 지수함수가 곱해진 형태의 함수 그래프를 빠르게 파악할 수 있으면 풀이가 한결 간단해집니다.





댓글