2022년 10월 고3 모의고사 수학(공통) 해설(등급컷, 오답률, 손글씨)

2022년 10월 12일(수) 전국연합 학력평가 수학 공통(수학 1, 수학 2) 문항에 대한 손글씨 해설입니다. 등급컷과 오답률도 함께 정리하였으니 참고해서 학습해주세요. 수학 선택과목(확률과 통계, 미적분, 기하)에 대한 해설은 아래 링크를 참고해주세요.

2022년 고3 모의고사 수학 손글씨 풀이

수학 이외의 과목의 문제와 해설은 '수능 및 모의고사 문제 및 해설(전과목)' 카테고리를 참고해주세요.

2022년 10월 고3 모의고사 수학 등급컷 및 오답률

선택과목에 따라 등급컷이 다릅니다. 출처는 ebs입니다.

등급	원점수			표준 점수	백분위	오답률(EBS)(문항번호/오답률)
등급	확률과 통계	미적분	기하	표준 점수	백분위	순위	확률과 통계	미적분	기하
1	82	78	80	138	96	1	22/96.1	22/96.1	22/96.1
2	69	66	68	127	89	2	30/89.9	30/91.8	20/89.3
3	59	56	57	118	77	3	23/89.3	20/89.3	21/87.2
4	43	40	41	104	60	4	21/87.2	21/87.2	30/82.9
5	26	23	24	89	40	5	29/83.6	15/81.9	15/81.9
6	18	15	16	82	23	6	15/81.9	29/78.7	29/81.0
7	14	10	11	78	12	7	14/76.4	14/76.4	14/76.4
8	10	7	8	75	5	8	28/64.6	28/70.7	13/59.3

2022년 10월 고3 모의고사 수학 손글씨 해설

4점짜리 문항은 손글씨 해설과 함께 간단한 코멘트를 남겼습니다. 수학 공통문항의 전체 손글씨 해설은 아래 파일로 첨부하였습니다. 학습에 참고해주세요.

2022년-10월-고3-수학-문제지.pdf

0.64MB

(2022)10월-고3-수학(공통)-손글씨해설.pdf

10.54MB

2022년 10월 고3 모의고사 수학 9번

다항함수 문제입니다. 다항함수는 기본적으로 차수와 계수를 찾아내야 합니다. 차수를 찾는 과정을 연습하기에 간단하면서도 좋은 문제입니다.

2022년 10월 고3 모의고사 수학 10번

지수함수 문제입니다. 두 가지 이상의 함수가 나오면 두 함수의 관계(역함수, 대칭)를 파악하여 문제에 활용하는 것이 좋습니다. 첫 번째 풀이는 수식 위주로 해결하였으며, 두 번째 풀이는 두 함수의 점 대칭 관계를 이용하여 풀었습니다. 첫 번째 풀이가 많이 접근할 수 있는 풀이이지만 두 번째 풀이에서 두 그래프의 관계를 파악하는 연습도 필요합니다.

2022년 10월 고3 모의고사 수학 11번

주기 함수, 함수의 연속을 이용하는 많이 볼 수 있는 문제입니다. 마지막 실근의 개수가 5개가 되도록 f(x) 그래프를 추론할 수 있어야 합니다.

2022년 10월 고3 모의고사 수학 12번

삼각함수 그래프 문제입니다. 절댓값을 풀어서 해결할 수 있습니다. x-파이/3a를 적절히 치환하여 해결할 수도 있으나 크게 복잡하지 않아 바로 풀이하였습니다.

2022년 10월 고3 모의고사 수학 13번

사인 법칙과 중학교 도형을 이용하는 문제입니다. 중학교 도형은 따로 학습하기보다 문제에 포함되어 나올 때마다 정리를 해두는 것이 좋습니다. (다)를 구하는 과정은 두 가지 방법으로 접근할 수 있으니 참고해주세요.

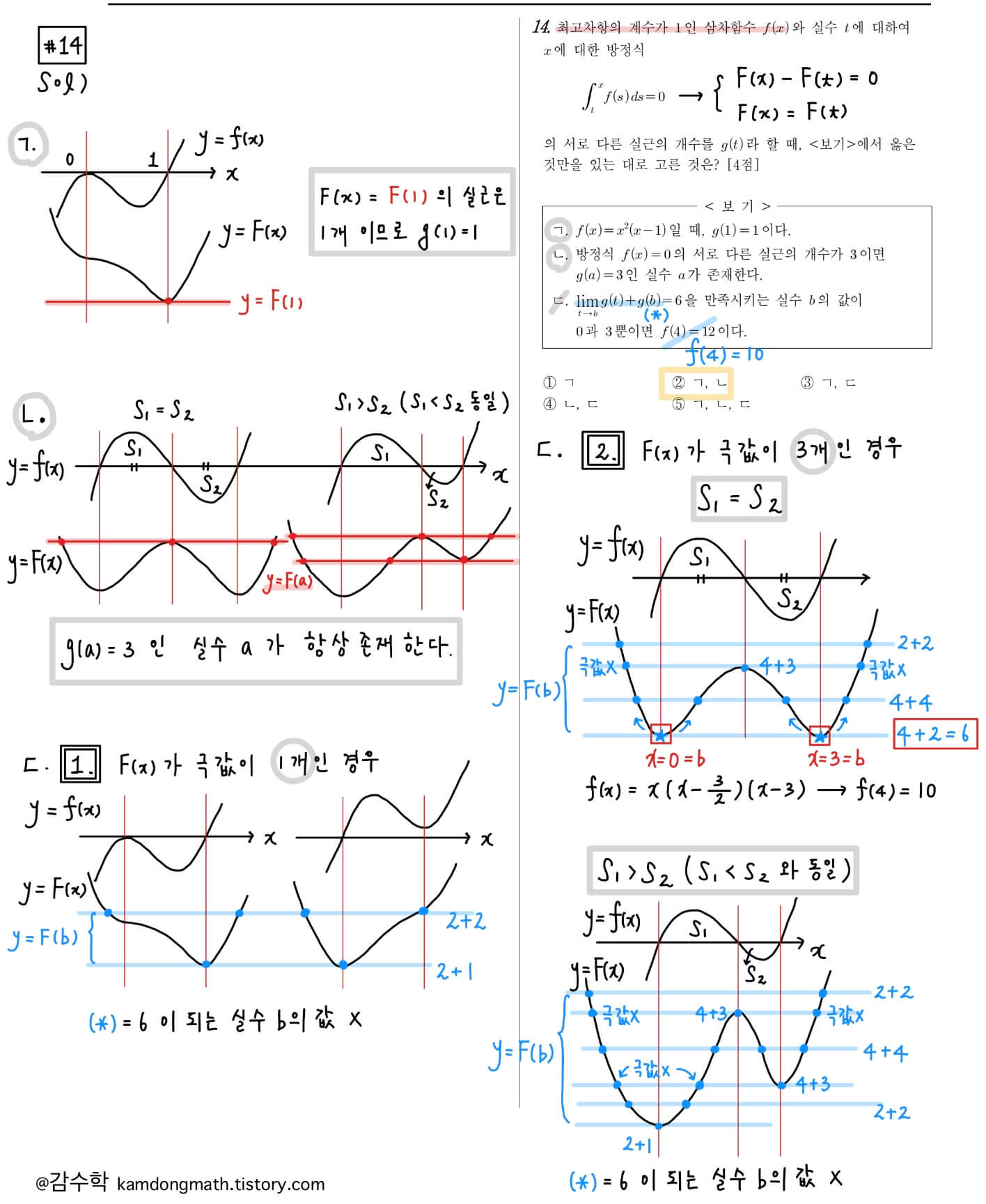
2022년 10월 고3 모의고사 수학 14번

정적분으로 정의된 함수 문제입니다. f(x)의 그래프에 따라 F(x)가 결정되고 F(x)와 F(t)의 실근의 개수를 F(x)의 그래프를 통해 판단할 수 있어야 합니다. ㄷ에 대해 최대한 자세히 풀이를 작성하였으니 참고해주세요.

2022년 10월 고3 모의고사 수학 15번

Sn을 함수로 보고 해결하는 자주 출제되고 있는 유형입니다. 자연수 p값을 1부터 대입해보면서 만족하는 최소의 p값을 추론할 수 있어야 합니다. Sn의 형태가 등차수열의 합과는 조금 다르게 상수항이 더해져 있으나 관찰을 통해 a2부터 등차수열을 만족하는 것을 알 수 있습니다. 마지막 q의 범위를 구할 때는 등호에 유의해야 합니다.

2022년 10월 고3 모의고사 수학 20번

수식, 그래프를 이용하여 두 가지로 풀이하였습니다. 이 문제에 대해서는 수식으로 푸는 것이 훨씬 간단하지만 아래와 같은 상황이 그래프로는 어떻게 해석할 수 있는지 파악하는 것도 매우 중요하니 두 번째 풀이도 꼭 참고해주세요.

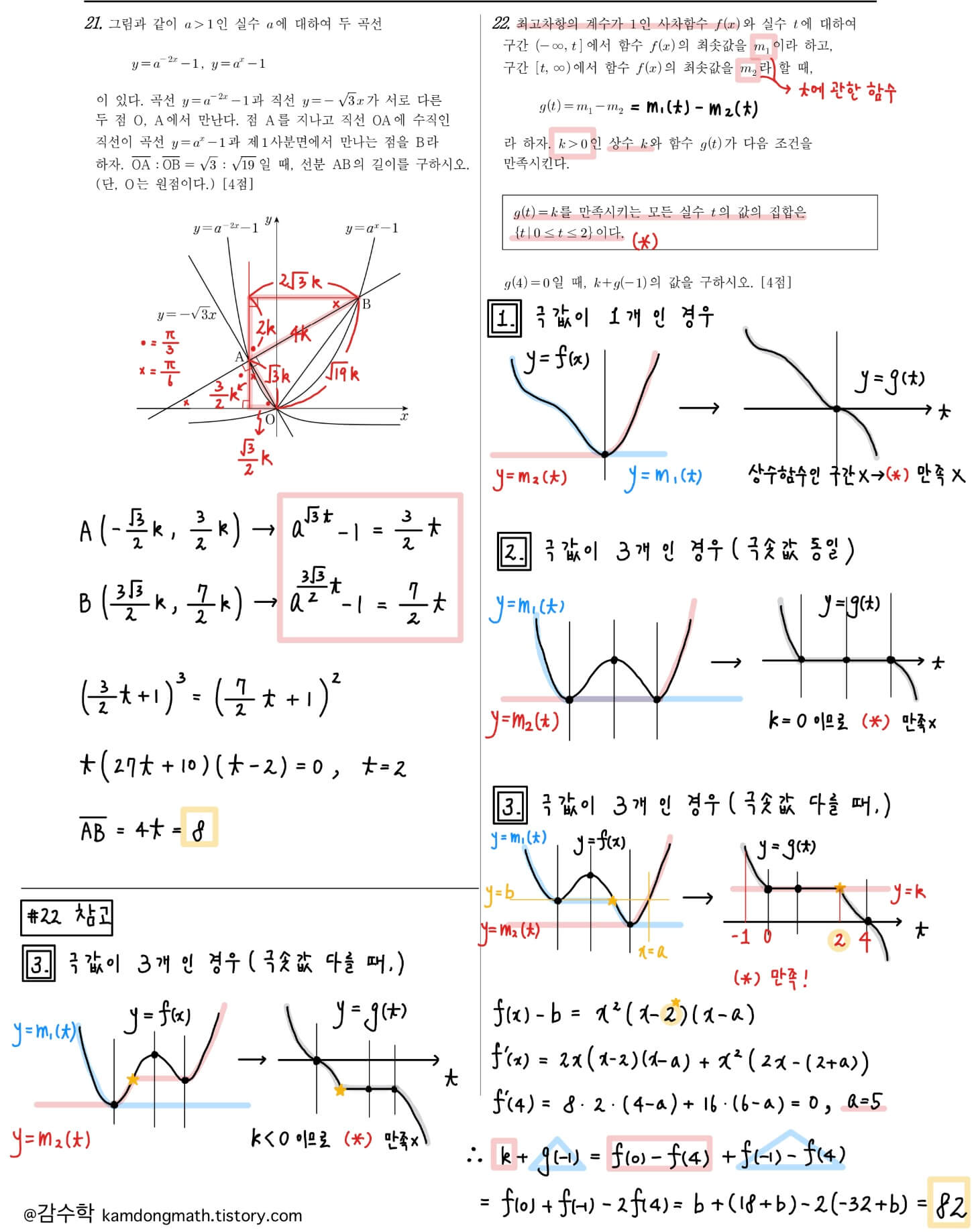
2022년 10월 고3 모의고사 수학 21번

함수의 기울기와 직각삼각형을 이용하여 A, B의 좌표를 나타내야 합니다. 보조선을 이용하여 직각삼각형을 만드는 방법은 알고 있는 각을 이용할 수 있도록 해야 합니다. 아래 풀이 이외에도 다른 방법이 있을 수 있으니 참고해주세요.

2022년 10월 고3 모의고사 수학 22번

오답률 1위 22번 문제입니다. 시간이 모자라 많은 학생들이 시도를 못했을 것으로 예상합니다. f(x)의 그래프에 따라 m1(t), m2(t)를 구할 수 있으며, 이에 따라 g(t) 그래프 개형을 구할 수 있습니다. 해설은 그래프 개형에 따라 분류하여 자세히 작성하였지만, 실전에서는 조건을 만족하는 그래프 하나만 찾으면 됩니다.