2023학년도(2022년) 수능 수학 공통 해설(손글씨, 등급컷, 오답률)

2023학년도 수능이 2022년 11월 17일(목)에 시행되었습니다. 수학 공통문항(1번~22번)에 대한 손글씨 해설, 등급컷, 오답률을 정리하였습니다. 문제의 출처는 교육과정 평가원, 등급컷과 오답률은 EBS를 참고하여 작성하였습니다. 수학 선택과목(확률과 통계, 미적분, 기하)에 대하 해설은 아래 링크를 참고해주세요.

2022년 고3 모의고사 수학 손글씨 풀이

2022년 고3 월 모의고사 수학 등급컷 및 오답률

선택과목 확률과 통계, 미적분, 기하에 따라 등급컷이 다릅니다. 문항별 오답률은 EBS를 참고하여 작성하였습니다.

등급	원점수			표준 점수	백분위	오답률(EBS)(문항번호/오답률)
등급	확률과 통계	미적분	기하	표준 점수	백분위	순위	확률과 통계	미적분	기하
1	88	84	88	135	96	1	29번/97.4%	22번/94.5%	22번/94.5%
2	79	75	78	127	89	2	30번/96.5%	30번/94.3%	30번/87.7%
3	70	66	69	118	77	3	22번/94.5%	14번/86.6%	14번/86.6%
4	55	51	54	107	60	4	14번/86.6%	29번/85.4%	21번/84.2%
5	35	31	33	92	40	5	21번/84.2%	21번/84.2%	29번/74%
6	21	17	19	80	23	6	15번/71.6%	15번/71.6%	15번/71.6%
7	16	12	13	76	12	7	20번/68.8%	20번/68.8%	20번/68.8%
8	11	7	8	72	4	8	12번/64.3%	12번/64.3%	12번/64.3%

2023학년도(2022년) 수능 수학 손글씨 해설

2023 수능 문제 파일, 직접 제작한 손글씨 풀이, EBS에서 제공한 풀이를 함께 첨부하였습니다. 주요 문항은 아래 사진과 함께 정리를 하였습니다. 전문항은 첨부파일을 참고해주세요.

2023-수능-수학-문제.pdf

1.01MB

2023-수능-수학(공통)-손글씨해설.pdf

11.42MB

2023-수능-수학-해설-ebs.pdf

0.46MB

2023학년도(2022년) 수능 수학 11번: 중학교 도형의 성질과 cos법칙, sin법칙을 이용하여 해결할 수 있는 문제입니다. 기출문제를 정리하면서 중학교 도형의 성질이 나올 때마다 정리해놓는 것이 좋습니다.

2023학년도(2022년) 수능 수학 12번: 극솟값의 정의와 주어진 그래프 모양을 바탕으로 f(x)를 추측하는 문제입니다. 그래프 추측을 연습하기 좋은 문제입니다.

2023학년도(2022년) 수능 수학 13번: 제곱근의 성질에 관한 문제입니다. 이런 문제의 경우 조금 헷갈릴 수 있지만 자연수라는 조건이 있어 하나씩 해보면 규칙과 성질을 발견하실 수 있습니다.

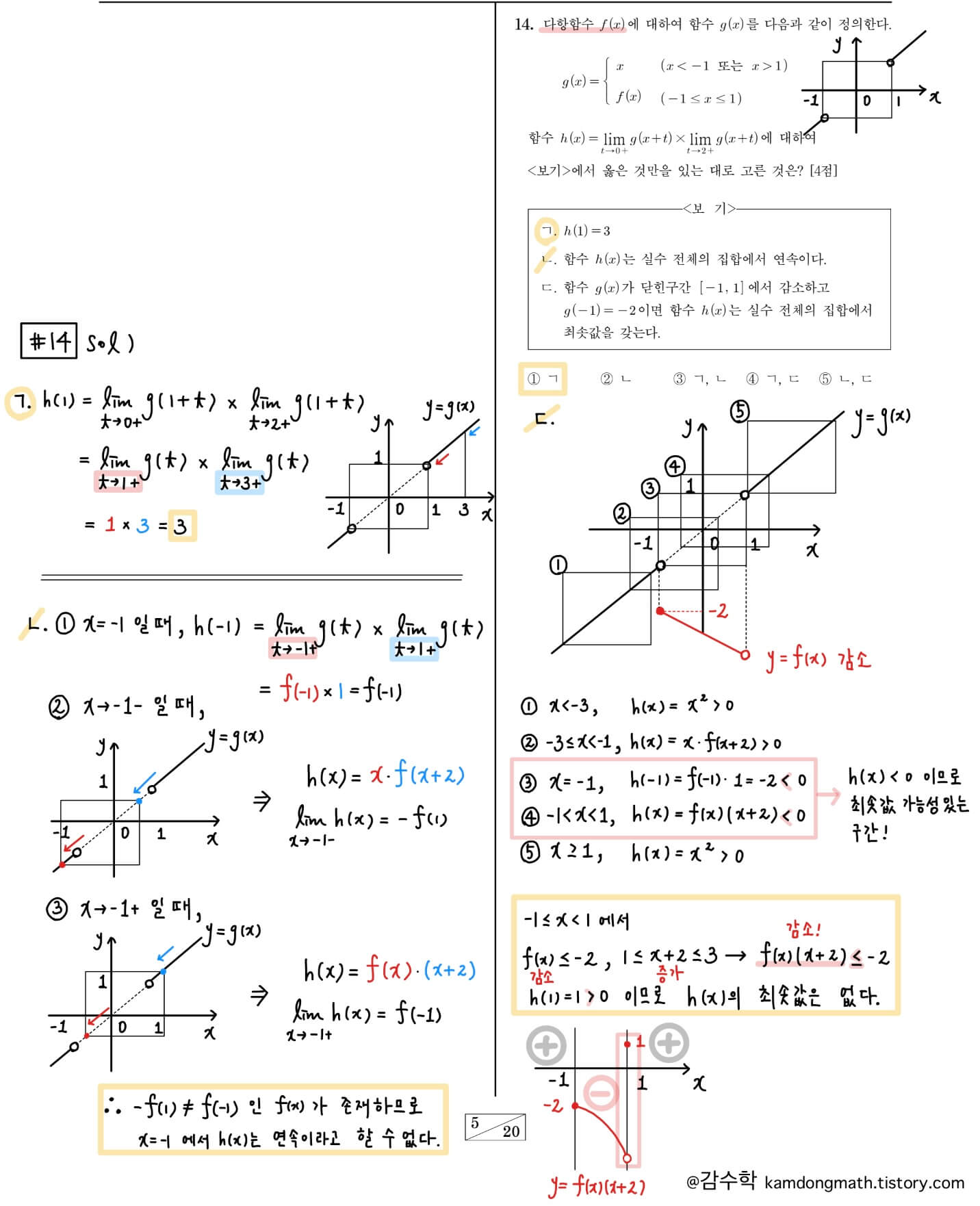
2023학년도(2022년) 수능 수학 14번: h(x)라는 함수가 극한으로 정의돼서 어렵게 느껴졌을 문제입니다. ㄴ에서는 연속성을 조사하기 위해 극한으로 정의된 함수의 극한을 생각하는 것이 쉽지 않았을 것 같고, ㄷ에서 제시된 형태의 최솟값이 없는 경우도 많이 보지 못한 경우라서 익숙하지 않았을 문제입니다.

2023학년도(2022년) 수능 수학 15번: 수열문제입니다. 기존의 수열 형태와 유사하며 3으로 나눈 나머지의 종류를 함께 생각해야 하는 문제입니다.

2023학년도(2022년) 수능 수학 21번: 지수, 로그함수 그래프를 생각하는 문제입니다. 예전의 격자점 개수 문제에서 많이 사용되는 사고 과정의 문제입니다. 문제 위치에 비해 쉽게 해결할 수 있는 문제입니다.

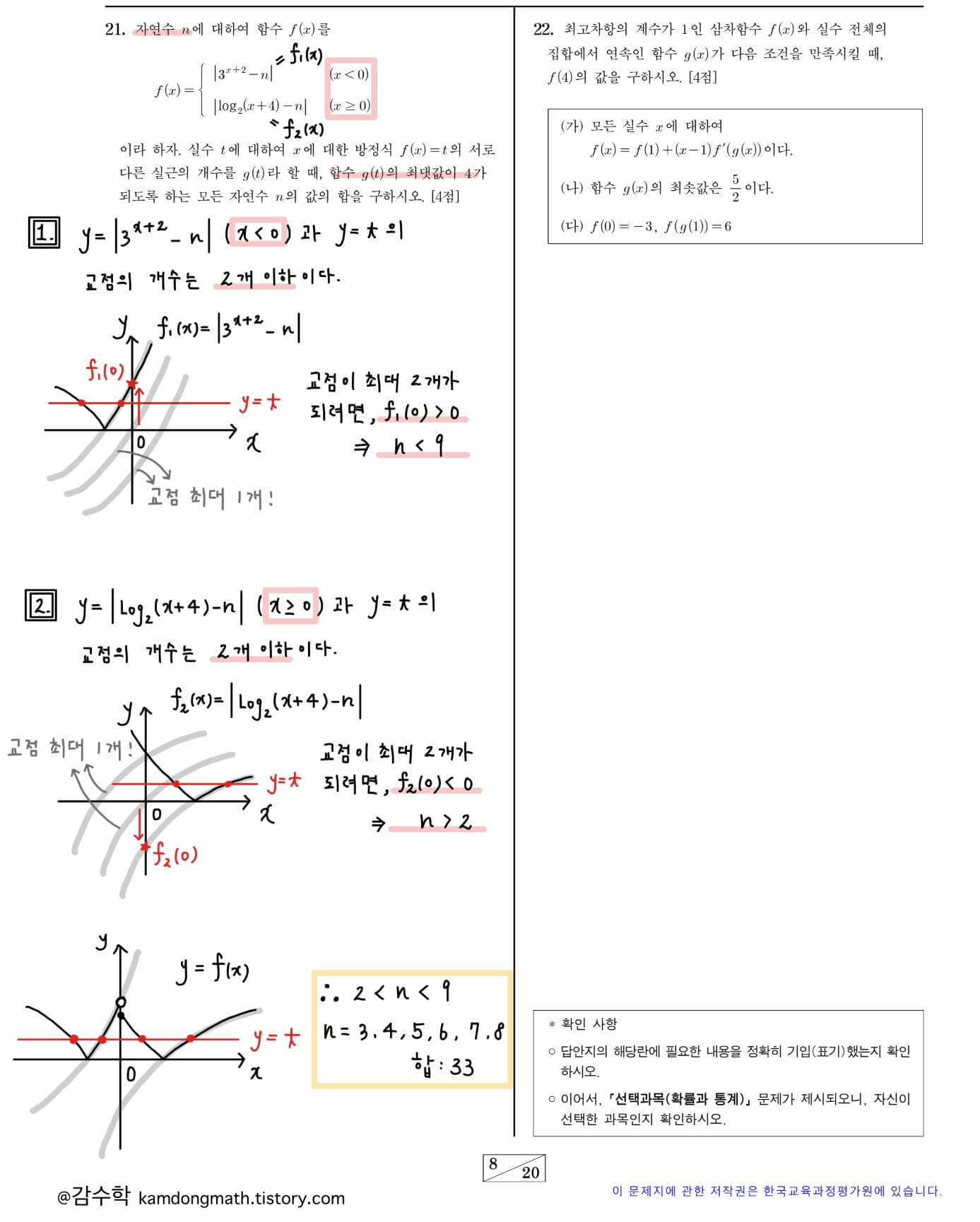
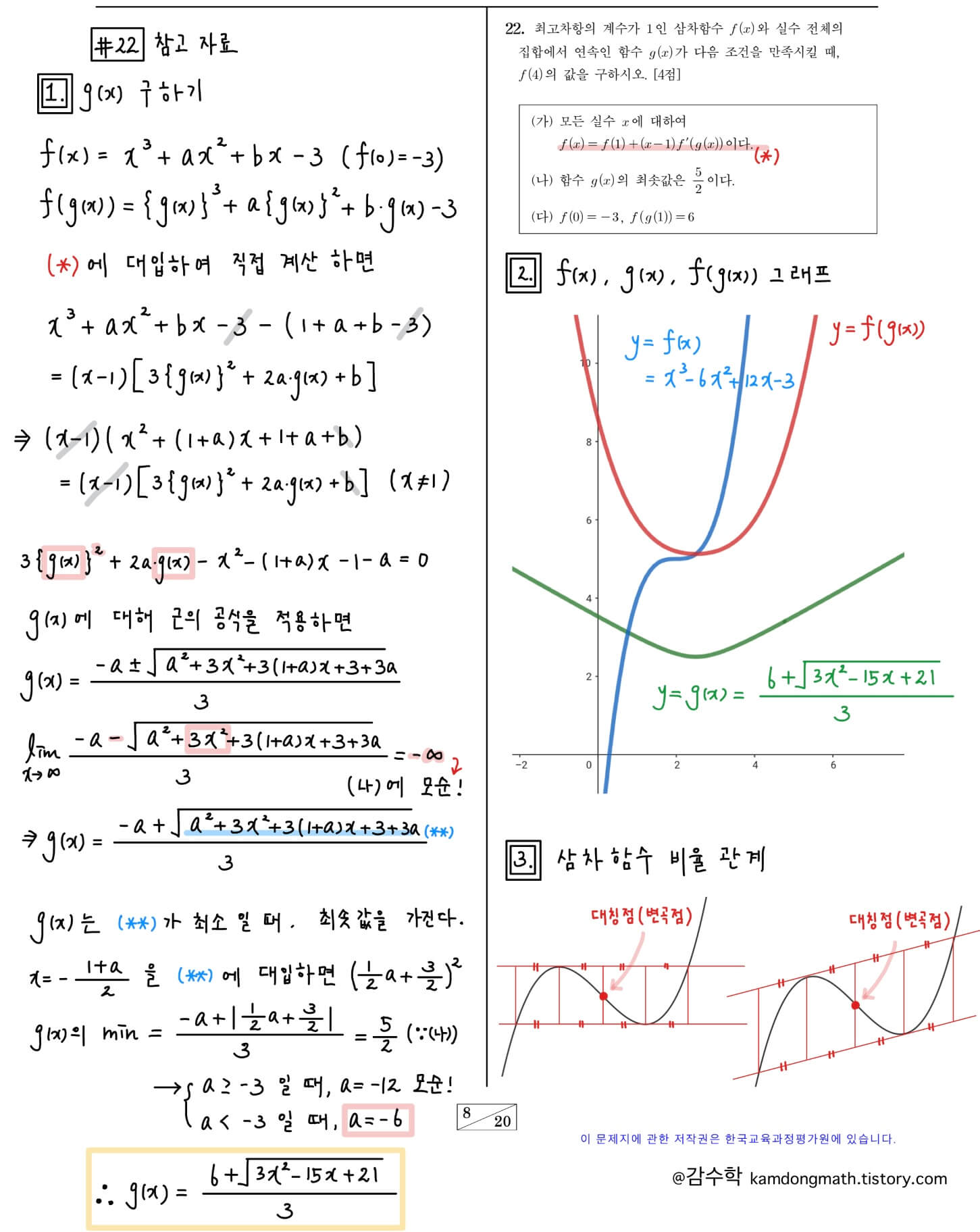
2023학년도(2022년) 수능 수학 22번: 평균 변화율과 합성함수에 관한 문제입니다. g(x)가 f'(x)의 정의역 역할을 하고 있습니다. (나) 조건을 잘 해결하는 것이 핵심입니다. 마지막 계산과정에서는 삼차 함수의 대칭점(변곡점)과 접점을 이용한 비율 관계를 사용하였습니다. 추가로 수식으로 g(x)를 직접 구하는 과정과 f(x), g(x), f(g(x))의 그래프를 첨부하였으니 참고해주세요.