2023년 고3 4월 모의고사(5월 10일 시행) 수학 선택과목 미적분(23번~30번) 손글씨 해설, 등급컷, 오답률을 정리하였습니다. 수학 공통문항(1번~22번), 확률과 통계, 기하에 대한 손글씨 해설은 아래 글을 참고해 주세요. 글의 순서는 다음과 같습니다.
2023년 4월 모의고사 수학(미적분) 등급컷 및 오답률
2023년 4월 모의고사 미적분 손글씨 해설
2023년 모의고사 미적분 손글씨 해설
2023년 4월 모의고사 미적분 등급컷 및 오답률
2023년 4월 모의고사 미적분 등급컷과 오답률(1위~15위)입니다. ebs에 공개된 내용을 정리하였으며, 오답률은 조사하는 기관에 따라 다소 차이가 있을 수 있습니다. 2023년 4월 모의고사 전 과목 문제와 해설은 아래 글에서 확인할 수 있습니다. 4월 모의고사 원점수 확정 등급컷은 성적표가 발표되면 블로그에 작성할 예정이니 참고해 주세요.
| 등급 | 원점수 | 표준 점수 |
백분위 | 오답률(EBS)(문항번호/오답률) | ||||||
| 미적분 | 순위 | 번호/오답률 | 순위 | 번호/오답률 | ||||||
| 1 | 73 | 136 | 96 | 1 | 30번/98.3% | 9 | 14번/61.9% | |||
| 2 | 63 | 126 | 88 | 2 | 22번/96.7% | 10 | 13번/57.9% | |||
| 3 | 55 | 118 | 77 | 3 | 29번/96.1% | 11 | 12번/56.9% | |||
| 4 | 42 | 106 | 60 | 4 | 21번/85% | 12 | 19번/48.1% | |||
| 5 | 26 | 90 | 40 | 5 | 20번/77.5% | 13 | 27번/46.4% | |||
| 6 | 17 | 81 | 24 | 6 | 28번/71.5% | 14 | 26번/41.6% | |||
| 7 | 12 | 77 | 11 | 7 | 15번/67.8% | 15 | 5번/40.4% | |||
| 8 | 9 | 74 | 4 | 8 | 11번/65.3% | |||||
2023년 4월 모의고사 미적분 손글씨 해설
2023년 4월 모의고사 미적분 손글씨 해설입니다. 문제지와 함께 교육청에서 제공하는 해설지도 함께 첨부하니 다양한 풀이를 함께 참고하시기 바랍니다.
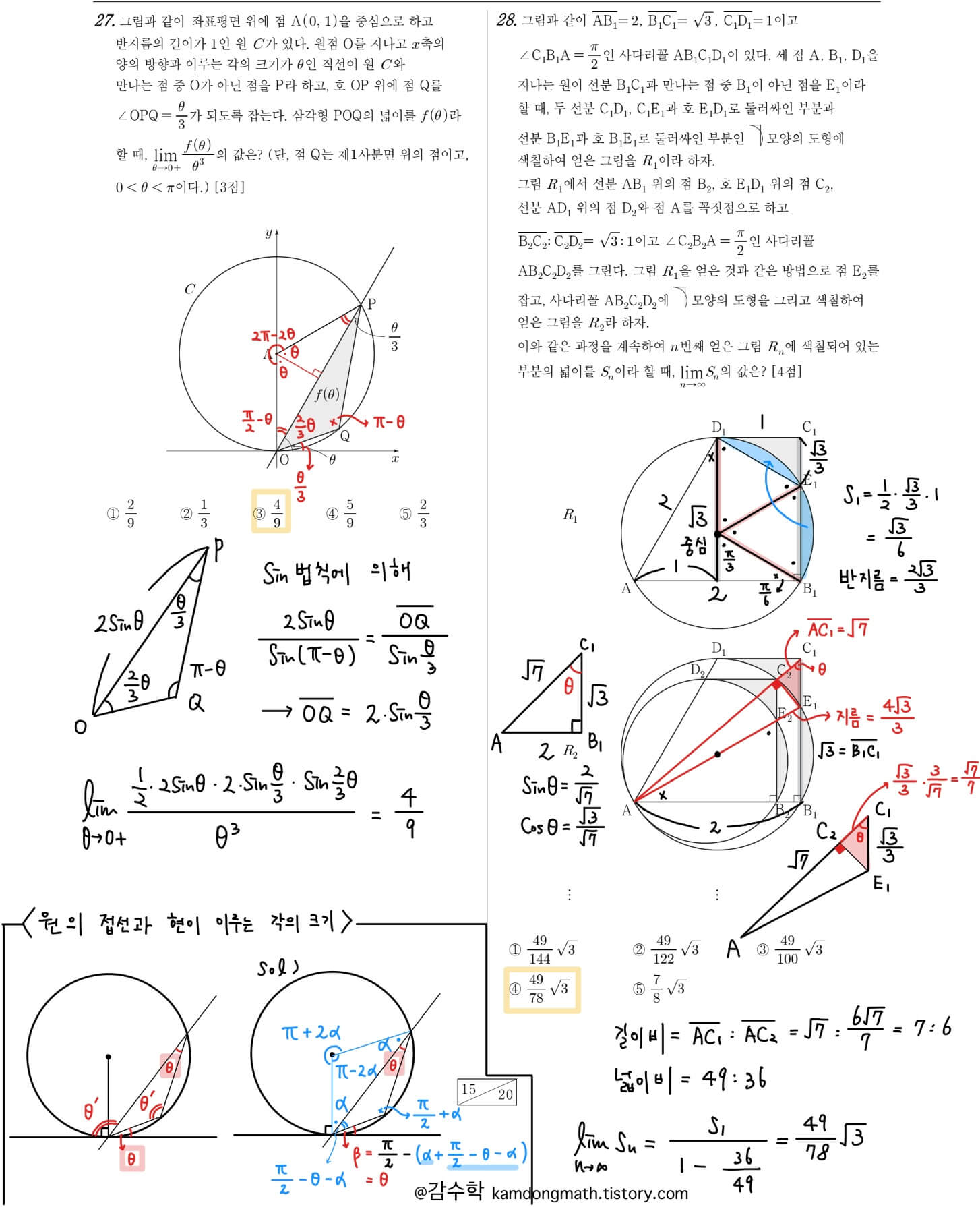
2023년 4월 미적분 27번: 함수의 극한과 도형이 결합된 문제입니다. 많이 출제된 유형의 문제이며 27번 문제도 3점짜리로 크게 어렵지는 않습니다. 중학교에서 학습한 원의 접선과 현이 이루는 각의 관계를 이용하여 삼각형 OPQ의 각을 파악할 수 있으며, sin법칙을 이용하여 정답을 구할 수 있습니다. 중학교 도형 내용도 아래 정리하였으니 참고해 주세요.
2023년 4월 미적분 28번: 무한등비급수와 도형이 결합된 문제입니다. 27번과 마찬가지로 많이 출제된 유형입니다. 합동인 활꼴을 찾아 S1을 구할 수 있으며, 공비를 구하는 과정에서는 직각 삼각형을 찾아 해결할 수 있습니다. 직각 삼각형을 찾는 과정도 중학교 도형의 원주각 중심각의 관계를 알고 있어야 합니다.
27번과 28번과 같은 유형을 2022년에 시행된 모의고사와 수능에서 따로 정리하였으니 참고해 주세요.
2023년 4월 미적분 29번: 삼각함수 덧셈정리 문제입니다. 마찬가지로 중학교 도형 개념이 포함된 문제이며, 현재 교육과정에서는 사라졌지만 반각공식을 이용하여 해결할 수 있습니다. 사실상 용어만 없어졌지 배각공식을 이용하여 유도하는 점을 보면 반각공식과 동일하므로 알아두는 것이 좋습니다. 다소 도형이 복잡하게 느껴질 수 있으나 풀이는 생각보다 간단합니다.

2023년 4월 미적분 30번: 오답률 1위 30번 문항입니다. (가)를 통해 주어진 범위의 그래프를 그릴 수 있어야 하며, (나)를 통해 평행이동, 대칭이동, 축소를 통해 모든 양수 범위의 그래프를 그릴 수 있습니다
g(x)를 구하는 과정에 있어서 미분계수의 정의를 그래프상에서 기울기로 생각하여 도함수의 극한으로 바꿔서 생각하였습니다. 실제 미분계수의 정의와 도함수의 극한은 다른 개념이지만 고등학교에서 다루는 함수 내에서는 같은 값을 가지므로 크게 문제 되지 않습니다.
아래 그래프에서는 도함수의 좌극한과 우극한을 나타내었으며, (*)를 구하는 과정에서는 4k+1, 4k+2, 4k+3, 4k+4에 따라 다른 값을 가지므로 나눠서 생각하였습니다. 상세한 풀이는 아래 사진을 참고해 주세요.





댓글